一言日記 2020/08/23（夏休み12日目）

CMOSアニーリングマシンのWeb APIの仕様を少し掴んだので，今日はイジングエディタをいじってた．

最適化問題からイジングモデルの落とし込みにある程度慣れれば大学院の研究のスタートラインに立てるはず．

ただ，今日は最適化問題ではなく単純な最小値探索問題をイジングモデルに落とし込もうとしてた．

問題サイズN=4では上手くいったがN=6では上手くいかなかった．

そもそも最小値探索問題は相互作用を考える余地がない問題な気がするので磁場（一体のパラメータ: 頂点）と相互作用（二体のパラメータ: 辺）を持つイジングモデルに落とし込むのに適切な問題ではないかもしれない．

まあとりあえずの練習ということで磁場を問題の入力（Annealing Cloud Web [1] では-3, -2, -1, +1, +2, +3を設定可能）として，出力のスピンが+1なら最小値，-1なら最小値ではないと考えることにした．

以下の画像では左上から時計回りに+3，+2，+1，-1を各ノード（ノードはおそらく量子を表している）にかかる磁場パラメータとし，スピンが+1を取ることを最小限に抑えるために相互作用パラメータを+1で与えている（相互作用考える余地がないと先ほど書いたがこの相互作用はイジングモデルに適合させるために無理やり追加した感があるので多分おそらくやはり適してない）．

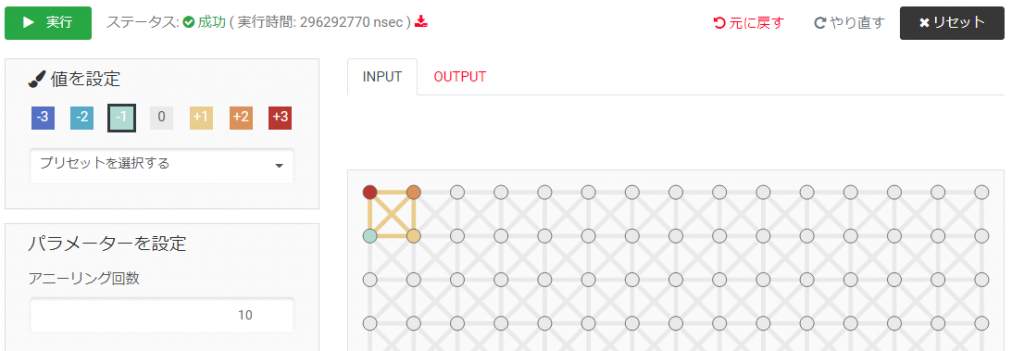
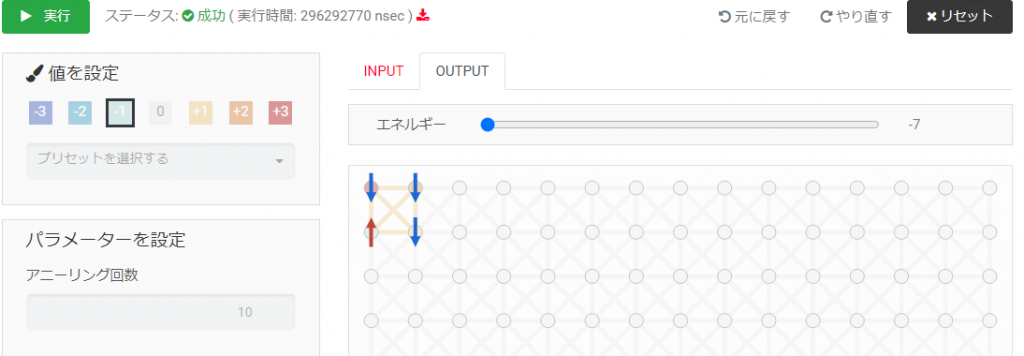
出力の上向きの赤矢印が+1，下向きの青矢印が-1を表している．

N=4のときは[+3, +2, +1, -1]の中で -1 の磁場パラメータを与えたノードが +1（最小値）となってくれた．



次はN=6のときの入力と出力だが，Nの数が増えてくると各ノードの全結合が簡単でなくなるので複数ノードによるチェインを行っている．

チェインというのは隣接した複数のノードを一つのノードとみなす手法で，これによりすべての各ノード間での相互作用パラメータの設定を可能としている．

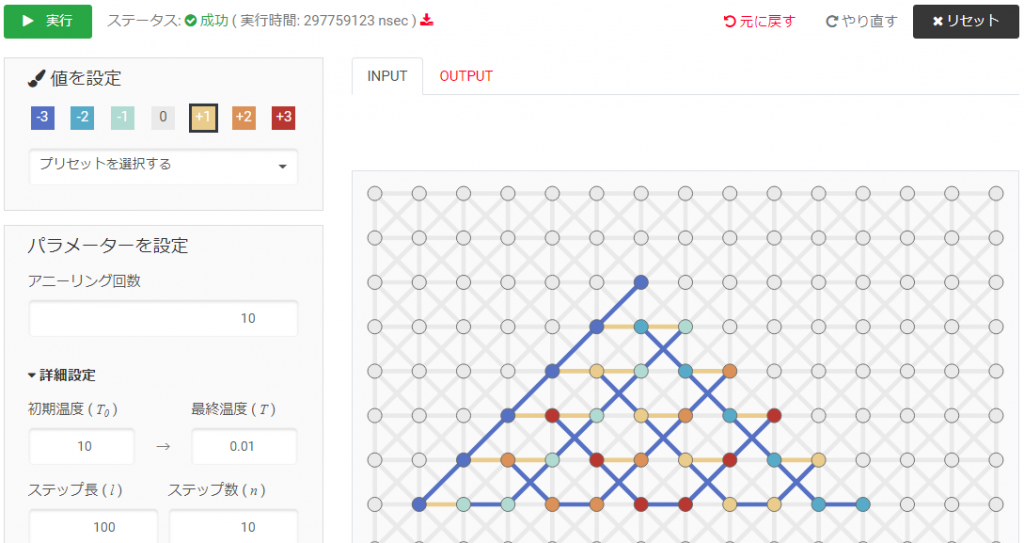
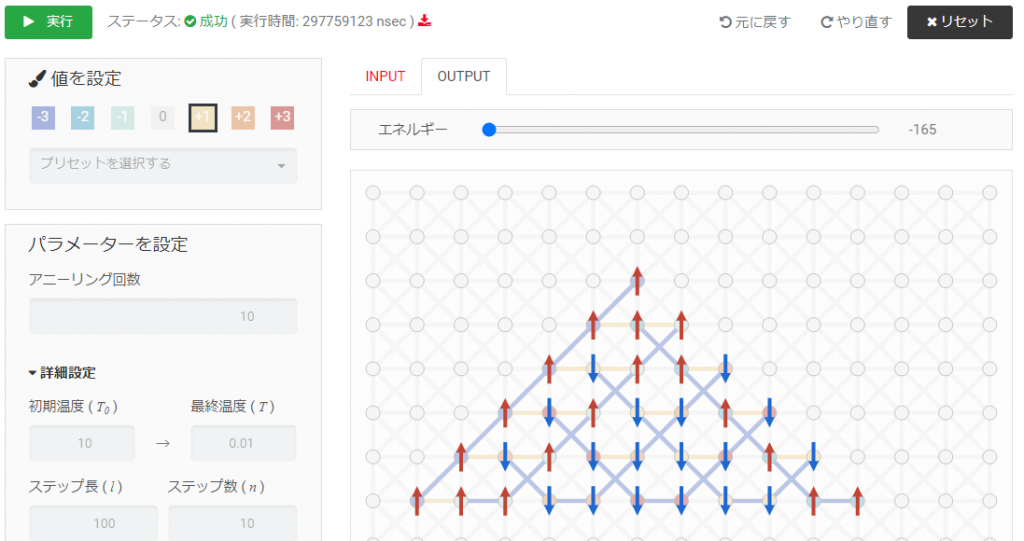
N=6のときは[+3, +2, +1, -1, -2, -3]の中で -1, -2, -3 の磁場パラメータを与えたノードが +1 となった．

-3 を与えたノードのスピンだけを +1 とするには制約条件を論理式で表してイジングモデルに落とし込んであげれば良さそう．

でもめんどくさそう中々上手くいかなかったので最小値探索問題はここまで．

次は最適化問題らしい問題をモデルに落とし込む練習をする．

参考にさせて頂いたサイト

[1] Annealing Cloud Web

[2] 技術リソース :: QUANTUM COMPUTER TECH RESOURCES